General Motion Tracking: A Scalable Framework for Unified Human Motion Control

Paper Reference: Chen, Z., Ji, M., Cheng, X., Peng, X., Peng, X. B., & Wang, X. (2025). GMT: General Motion Tracking for Humanoid Whole-Body Control. arXiv preprint arXiv:2506.14770.

Note: This blog post represents my personal notes and understanding after reading the GMT paper. It is not an official summary or endorsement by the original authors. Any errors or misinterpretations are my own responsibility.

A scalable framework enabling a single, unified policy to track a massive diversity of human motions without needing separate policies for each skill.

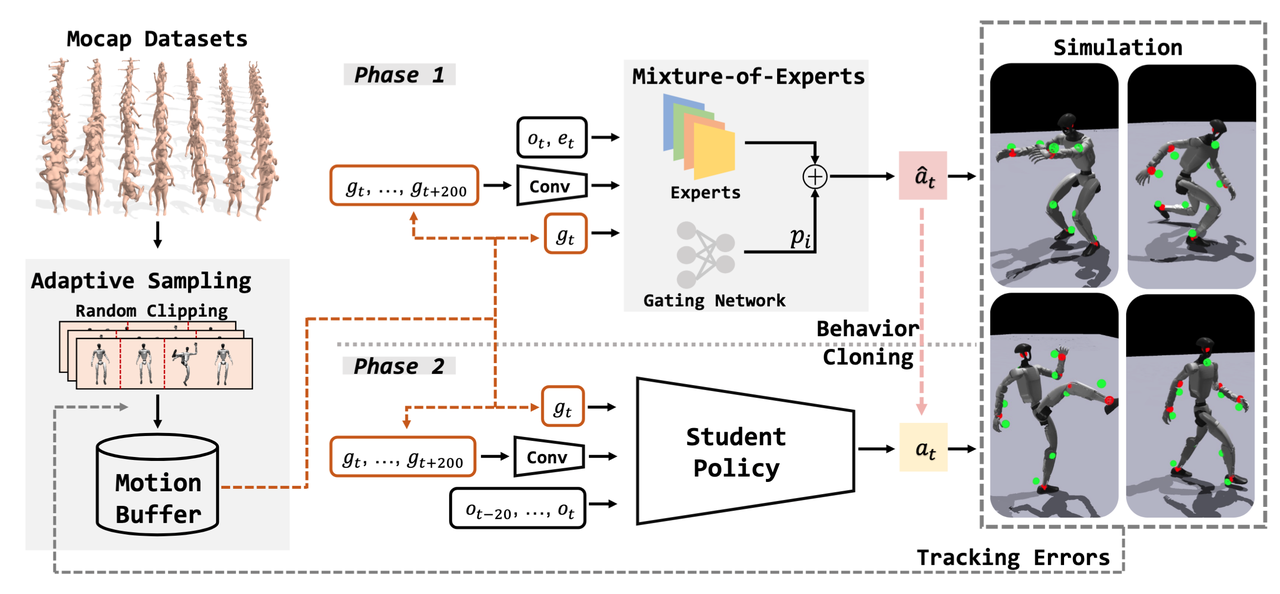
An overview of GMT

Framework

Data Preparation (Adaptive Sampling)

This module addresses the issue of data imbalance. In large datasets (like AMASS), simple motions (walking/standing) are over-represented, while complex motions (backflips/kicking) are rare.

MoCap Datasets: The system ingests massive human motion capture data.
Motion Buffer & Random Clipping: The data is chopped into short clips and stored in a buffer.
Adaptive Sampling:
- Normally, data is sampled uniformly. In GMT, the system uses Tracking Errors (feedback from the simulation on the right) to adjust sampling probabilities.
- If the robot fails to track a specific motion (high error), that motion is sampled more frequently in the next batch. This forces the policy to focus on “hard” examples, ensuring the robot doesn’t just learn the easy stuff.

Completion Level $c_1$:

Definition: Represents the robot’s mastery of a specific motion $i$.

Decay Process: It initializes at 10 (unlearned) and decays by a factor of 0.99 every time the robot successfully completes the motion, until it reaches a minimum of 1 (mastered).

Function: Serves as a counter for the “curriculum phase.” High $c_i$ implies the robot is still in the early stages of learning this specific skill.

Dynamic Error Threshold ($E_i$) - The Curriculum

Formula: $E_i=0.25\exp\left( \frac{c_i-1}{9}\times \log\left( \frac{0.6}{0.25} \right) \right)$

Purpose: Determines the termination criteria for an episode.

Behavior:

Early Stage ($c_i=10$): $E_i\approx 0.6$. The system is lenient, allowing large tracking errors to prevent termination during initial learning.

Mastered Stage ($c_i=1)$: $E_i=0.25$. The system becomes strict, requiring high-precision tracking.

Sampling Weight ($s_i$) This determines how likely motion $i$ is to be selected in the next training batch. It is defined by a piecewise function:

Case A: Learning Phase ($c_i>1$):

\[s_i=c_i\]

Logic: Unmastered motions have high weights (up to 10), ensuring they are sampled frequently to accelerate learning.

Case B: Mastered Phase ($c_i=1):$

\[s_i=\left( \min\left( \frac{E_{\text{max\_key\_body\_error}}}{0.15}, 1 \right) \right)^5\]

Logic: This acts as Hard Negative Mining.

It uses a 5th-power function to aggressively penalize high errors.

If a “mastered” motion still produces high errors (near 1.0), the weight remains high ($1^5=1$).

If the error is low (e.g., 0.5), the weight vanishes ($0.5^{5}\approx 0.03$), preventing the waste of computational resources on already perfected skills.

Final Probability The actual sampling probability $P_i$ is obtained by normalizing the weights:
\[P_i=\frac{s_i}{\sum s_j}\]

By applying Adaptive Sampling from the start of training, we avoid repeatedly sampling easy segments of long motions and focus training efforts on refining performance on harder motions with higher tracking errors

Phase 1 (Teacher Training via RL)

Motion Mixture-of-Experts (Motion MoE) is a core mechanism within the GMT framework designed to enhance the expressiveness of the “Teacher Policy”.

Core Components

The Motion MoE is not a single network but an architecture composed of two main parts:

Group of Expert Networks:
- These are multiple parallel sub-networks (Experts).
- Each expert can be viewed as an independent policy that specializes in handling different types of motion patterns.
- They receive the robot’s state observation and motion targets as input, and each outputs a proposed action vector $a_i$.
Gating Network:
- This acts as the system’s “commander” or “router”.
- It receives the exact same input observations as the experts.
- Its output is a Probability Distribution, i.e., a set of weights $p_i$. These weights determine how much the system should trust a specific expert at the current moment.

Workflow (Pipeline)

Input
- $o_t, e_t$: The robot’s current proprioceptive state and tracking errors.
- $g_t$: The target pose for the current frame.
- $g_t, \ldots ,g_{t+200}$: Future trajectory information for the next 200 frames (processed via a Convolutional Neural Network / Conv).
Distribution: This information is fed simultaneously into the “Gating Network” and all “Expert Networks.”
Expert Computation: Each expert network calculates what it believes to be the optimal action $a_i$ based on the input.
Weight Assignment: The Gating Network analyzes the current state to determine which motion mode is most relevant (e.g., if the motion is “walking,” Expert A might get a higher weight; if it is “backflipping,” Expert B might be prioritized) and outputs weight $p_i$.

\[\hat{a}=\sum_{i=1}^{n}p_{i}a_{i}\]

When the model performs Backpropagation to minimize the loss function $\mathcal{L}$ (i.e., action error), we need to calculate the gradients for the expert network parameters $\theta_{i}$. According to the Chain Rule:
\[\frac{\partial L}{\partial \theta_{i}}=\frac{\partial L}{\partial a}\cdot \frac{\partial a}{\partial a_i}\cdot \frac{\partial a_i}{\partial \theta_i}\]
Based on the summation formula above, we can derive:
\[\frac{\partial a}{\partial a_i}=p_i(s)\]
This implies:
\[\text{Gradient update for Expert} i\propto p_i(s)\times \text{Total Error Signal}\]
The weight $p_i(s)$ determines the learning speed of Expert $i$.

How does Specialization “Emerge”?

Phase 1: Random Initialization

Initially, all experts are randomly initialized, and weights $p_i$ are also random (close to a uniform distribution).

However, due to randomness, for a specific motion (e.g., “Squatting”), Expert A might conincidentally output a result that is slightly better (slightly lower error) than Expert B.

Phase 2: Gating Network Bias

Increased Weeight: The next time “Squatting” is encountered, Expert A’s weight $p_A$ is larger (e.g., increasing from 0.25 to 0.3).

Amplified Gradient: According to the gradient formula above, Expert A receives a larger gradient update signal (because it has a higher weight, it bears more responsibility).

Accelerated Learning: Expert A learns how to optimize the “Squatting” motion faster.

Widening Gap: Expert A becomes increasingly proficient at “Squatting,” while other experts receive almost no gradient signal for “Squatting” due to their low weights ($p_i$is small). Consequently, they stop learning this motion and may even “forget” it.

Phase 4: Specialization

After thousands of iterations, Expert A becomes the “Squatting Specialist.”

Similarly, Expert B might perform slightly better during the initial phase of “Running,” and is thus locked in as the “Running Specialist.”

Why Don’t All Experts Learn the Same Thing? (Mode Collapse)

This involves a deeper mathematical intuition: The Non-convexity of the Loss Function.

If all experts did the exact same thing, they would effectively degenerate into a single large netwrok. However, different motions often have conflictiny dynamics:

Walking: Requires compliant leg joints(Low Stiffness).

Kicking: Requires explosive leg joints (High Stiffness).

If a single network tries to learn both simultaneously, it will learn the average, resulting in mediocre performance for both and a high total Loss. Conversely, if these two tasks are split between different experts, the total Loss is significantly reduces. Since the Optimizer essentially seeks the lowest point of Loss, it naturally tends to push conflicting tasks to different parameter groups, thereby achieving “division of labor.”

Phase 2 (Student Distillation via Behavior Cloning)

Core Objective: In Phase 1, although the Teacher Policy is powerful, it has flaws that prevent direct deployment on real hardware:
- Reliance on Privileged Information: The Teacher relies on the MoE architecture and explicit access to exact error $e_t$ and perfect future information.
- Complex Architecture: The MoE contains multiple expert networks and a gating network, which is computationally heavy and may not meet the high-frequency control requirements (e.g., 200Hz) of real robots.
- Lack of Robustness: Real-world sensors are noisy, and single-frame observations are often insufficient to infer velocity and contact states.

The goal of Phase 2 is to “compress” the Teacher’s capabilities into a structurally simple (usually a standard MLP) and input-realistic (history-dependent) Student network.

Input (Observation Space):
- Future Goals ($g_t, \ldots , g_{t+200}$): The Student still needs to know the future reference trajectory (processed via a Conv encoder). This tells the robot “where to go.”
- Historical Observations ($o_{t-20}, \ldots , o_{t} $): While the Teacher only looks at the current frame $o_t$, the Student looks at a history of the past 20 frames.
  - Principle: By stacking historical frames, a standard neural network can implicitly infer the robot’s velocity, acceleration, foot contact states, and environmental friction, without needing explicit sensor measurements.
Output (Action Space):
- $a_t$: Target Joint Positions, sent directly to the PD controller.

Mathematical Principle: Behavior Cloning

Phase 2 training no longer uses Reinforcement Learning (RL) reward functions. Instead, it uses Supervised Learning.

Loss Function

The Student network’s goal is to mimic the Teacher network’s output as closely as possible. Mathematically, this is achieved by minimizing the distance between the Student’s action $a_{\text{student}}$ and the Teacher’s action $\hat{a}_{\text{teacher}}$.

The loss function $\mathcal{L}$ is typically defined as the Mean Squared Error (MSE) or L2 norm:
\[\mathcal{L}(\theta_S)=\mathbb{E}_{s\sim\mathcal{D}}\left[ \| a_{\text{student}}(s_{\text{history}}, g_{\text{future}};\theta_S)-\hat{a}_{\text{teacher}}(s_{\text{current}}, g_{\text{future}})\|^2 \right]\]
Where:

$\theta_S$: The parameters (weights) of the Student network.

$s_{\text{history}}$: The sequence of historical observations seen by the Student ($o_{t-20}, \ldots , o_{t}$).

$\hat{a}_{\text{teacher}}$: The “ground truth” action output by the Teacher at the same moment.

$\mathcal{D}$: The distribution of data sampled from the simulation.

By optimizing $\theta_S$ via gradient descent, the Student gradually learns: “Given this history, I should do exactly what the Teacher would do.”

Full Pipeline:

Data generation (Rollout):

The trained Teacher Policy controls the robot in the simulation.

Detailed data is recorded for every frame:

Teacher’s input (current state).

Teacher’s perfect output $\hat{a}_t$ (the Label).

Student’s input (historical observations: sequence $o_{t-20}, \ldots , o_t$).

Distillation Training

Feed the recorded data into the Student Policy.

Forward Pass: The Student predicts action $a_{t}$ based on history.

Loss Calculation: Compare the difference between $a_t$ and $\hat{a}_t$.

Backpropagation: Update the Student network’s weights.

DAgger (Dataset Aggregation)

To prevent Distribution Shift (where the Student makes a small mistake, enters a state the Teacher never visited, and fails), DAgger is often used.

Mixed Control: During data collection, the Student is allowed to control the robot. When it is about to fall or deviate, the Teacher takes over to correct it.

This collects “correction” data, teaching the Student: “if you deviate, here is how to recover.”

Sim-to-Real Deployment:

Once training is complete, only the Student Policy weights are exported.

This network is lightweight, fast, and does not rely on privileged info, making it ready for deployment on real robot hardware.

Feature	Phase 1: Teacher	Phase 2: Student
Architecture	Mixture-of-Experts (MoE)	Standard MLP / Transformer
Input Data	Current state $o_t$ + Error $e_t$	Historical Observations $o_{t-20}, \ldots ,o_t$
Learning Method	Reinforcement Learning (RL / PPO)	Supervised Learning (Behavior Cloning)
Role	Explore limits, learn perfect motion	Compress knowledge, adapt to real sensors
Deployment	Simulation Only	Real-World Deployment

Simulation & feedback

Simulation: During data collection, the Student is allowed to control the robot. When it is about to fall or deviate, the Teacher takes over to correct it.
Visuals: The green/red dots on the robot represent keypoint tracking.
- Green: Good tracking (low error).
- Red: Poor tracking (high error).
Tracking Errors: The difference between the robot’s pose and the reference motion is calculated. This error signal is sent all the way back to the Adaptive Sampling module to update the training curriculum (closing the loop).

Motion Input

The Immediate Motion Target ($g_t$)

This vector represents the specific target state for the robot at the current frame $t$.

Symbol	Component	Dimension	Description & Key Features
$q_t$	Joint Positions	$\mathbb{R}^{23}$	The target angles for all the robot’s actuated joints.
$v_{t}^{\text{base}}$	Base Velocities	$\mathbb{R}^{6}$	Includes both linear and angular velocities of the robot’s base (torso/pelvis)
$r_{t}^{\text{base}}$	Base Orientation	$\mathbb{R}^{2}$	Specifically the Roll and Pitch angles of the base.
$h_{t}^{\text{root}}$	Root Height	Scalar	The vertical distance of the root (pelvis) from the ground.
$p_t^{\text{key}}$	Key Body Positions	$\mathbb{R}^{3\times K}$	The 3D positions of key body parts (e.g., hands, feet).

Note: Yaw is excluded to ensure the policy is invariant to the robot’s absolute heading.

Crucial Feature: These are Local coordinates aligned relative to the robot’s heading direction (unlike prior works that used global positions).

The Final Policy Input Structure

The final input fed into the neural network (Expert Networks) combines the immediate target with long-term future trends.

Component	Source / Calculation	Dimension	Purpose in GMT
Immediate Target ($g_t$)	Direct frame data at time $t$.	Vector	Explicit Tracking: Provides the exact pose required for the very next moment, ensuring high-precision control.
Latent Trend ($z_t$)	Source: Stacked future frames [$g_t, \ldots ,g_{t+100}$] (approx. 2 seconds). Process: Compressed via a Convolutional Encoder.	$\mathbb{R}^{128}$	Long-term Planning: Captures the high-level motion intentions (e.g., “accelerating,” “preparing to jump”) that single-frame data cannot reveal.