Average Distance Between Two Random Points in a Square

What’s the average distance between two randomly and uniformly chosen points in a unit square? That is, given a unit square , two random points and , where in Cartesian coordinates, we are asked to find out the average distance (or expected value ) between and .

To find the average distance, we first use Cartesian coordinates to express the distance between the points. The distance can be expressed using Pythagorean Theorem:

Given the distance formula between the two points, the average distance is actually the quadruple integral of :

Notice that the quadruple integral has four variables, we can simplify it by viewing and as and , since the distribution of the difference between two variable can be derived using triangular distribution formula, the probability density function (PDF) is , we can briefly prove this by first considering its cumulative density function (CDF):

the region 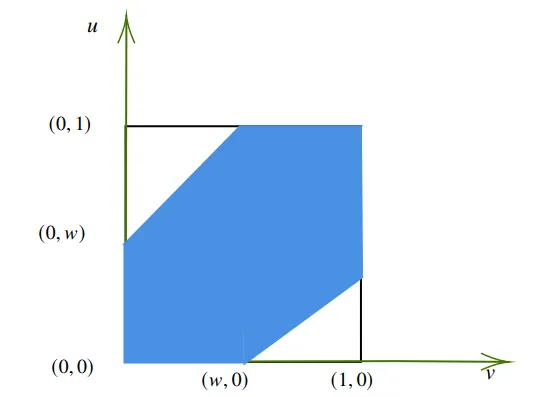can be given as follow:

Since PDF is the derivative of CDF:

Therefore the average distance can be expressed as:

using polar coordinates substitution :

then the Jacobian Matrix is:

therefore,

we’ll then use integral of the secant cubed:

hence,

similarly, average distance between two random points in a cube is:

Further Reading

• Triangular Distribution
• Integral of Secant Cubed